The COS function in Excel is a powerful tool for trigonometric calculations, providing users with the ability to determine the cosine of an angle. Whether you’re working on mathematical modeling, engineering simulations, or financial analysis, the COS function enables precise calculations involving angles. By simply inputting the desired angle in radians, users can quickly obtain accurate cosine values, facilitating various computations and analyses. Whether you’re calculating forces in physics problems, designing intricate geometrical shapes, or evaluating periodic trends in data, the COS function in Excel offers unparalleled flexibility and accuracy. Leveraging this function enhances the capabilities of Excel for advanced mathematical operations, empowering users to tackle complex tasks with ease and efficiency. With the COS function, Excel becomes an indispensable tool for professionals across various fields, providing unparalleled versatility and precision in trigonometric calculations.
This Tutorial Covers:
- What is COS function
- Syntax of COS function
- Arguments of COS function
- Usage notes of COS function
- Remark
- How to use COS Function in Excel
- Example 1 – How to calculate the value of cos (0)
- Example 2 – How to calculate the value of cos (30)
- Example 3 – How to calculate the value of cos (45)
- Example 4 – How to calculate the value of cos (60)
- Example 5 – How to calculate the value of cos (90)
- Usage of COS Function in Excel VBA
- VBA Example 1
- VBA Example 2
1. What is COS function in Excel?
The COS function is a built-in mathematical function in Excel that calculates the cosine of an angle in radians. It returns the ratio of the adjacent side of a right triangle to its hypotenuse, where the hypotenuse is the longest side of the triangle and the angle is measured in radians. The COS function is commonly used in trigonometry, physics, and engineering to solve a variety of problems, such as calculating distances and angles.
Microsoft Excel comes with this feature built-in In Microsoft Excel, it falls under the Math functions category. A given angle in radians is returned together with its cosine by the function. The value of the angle for which the cosine is to be calculated is the parameter. The angle can be determined by multiplying by PI()/180 or using the RADIANS function.
-
Syntax of COS function:
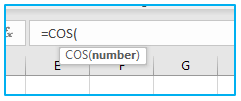
The Excel COS function’s syntax is as follows:
=COS(number)
-
Arguments of COS function:
Excel COS formula has one argument, which is a necessary input.
number- This is a necessary input. The angle at which the cosine is to be calculated is indicated.
2. Usage notes of COS function:
The COS function calculates the cosine of an angle given in radians, which represents the ratio of an adjacent side of a right triangle to its hypotenuse. The resulting value is between -1 and 1, and it can be used in trigonometry, physics, and engineering applications. For instance, if you provide an angle of PI()/6 radians (30 degrees), the COS function will return a value of 0.866, which represents the ratio of the adjacent side to the hypotenuse in a right triangle.
-
Remark:
To use the COS function with an angle given in degrees, you can either multiply the angle by PI()/180 to convert it to radians or use the RADIANS function to make the conversion automatically. This is because the COS function only accepts angles in radians, so you need to convert the angle from degrees to radians before using it in the function.
3. How to use COS Function in Excel?
The COS can be utilized in Excel workbooks via Excel VBA and the Worksheet (WS) function. It can be included in a worksheet cell’s COS formula as a WS function. It can be written into the VBA code as a VBA function.
For a better understanding, refer to the examples provided below.
-
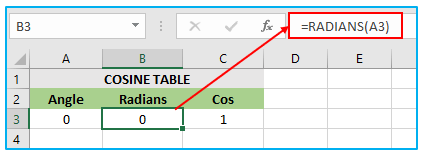
Example 1 – How to calculate the value of cos (0)
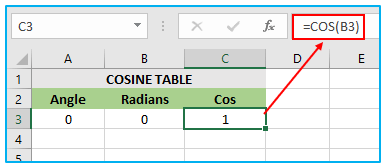
In this scenario, cell A3 contains the angle value for which the cosine needs to be calculated. The cell B3 contains the COS formula with the RADIANS function applied to cell A3. The result of RADIANS(A3) is 0, which is then used as the input for the COS formula in cell C3. As the COS function applied to 0 is equal to 1, the value of cell C3 is 1.
Therefore, the final value of cell C3 is 1, which is obtained by applying the COS function to the angle value of 0 in cell A3 after converting it to radians using the RADIANS function in cell B3.
-
Example 2 – How to calculate the value of cos (30)
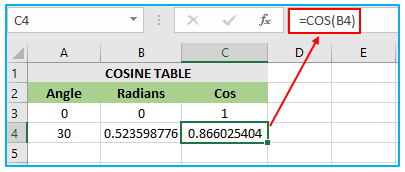
In this scenario, the angle value for which the cosine needs to be calculated is present in cell A4. The COS formula is associated with cell B4, which utilizes the RADIANS function to convert the angle value in cell A4 into radians. The result of RADIANS(A4) is 0.523598776. The COS function is applied to 0.523598776, which results in the value 0.866025404, and this value is assigned to cell C4.
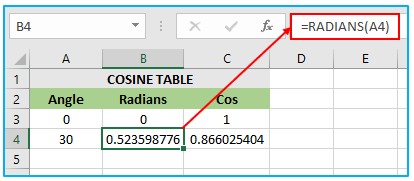
Thus, the final value of cell C4 is 0.866025404, which is obtained by applying the COS function to the angle value of 0.523598776 in cell A4 after converting it to radians using the RADIANS function in cell B4.
-
Example 3 – How to calculate the value of cos (45)
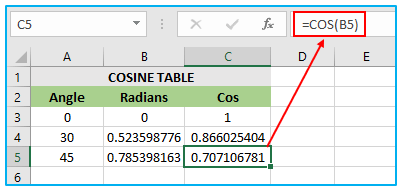
In this scenario, cell A5 contains the angle value for which the cosine needs to be calculated. The cell B5 has the COS formula with the RADIANS function applied to cell A5. The result of RADIANS(A5) is 0.523598776. The COS function is applied to 0.785398163, which is equal to 0.707106781. This value is assigned to cell C5.
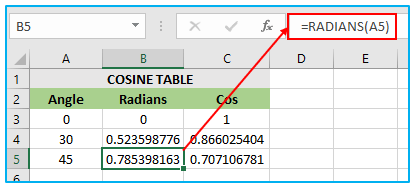
Thus, the final value of cell C5 is 0.707106781, which is obtained by applying the COS function to the angle value of 0.523598776 in cell A5 after converting it to radians using the RADIANS function in cell B5. The value 0.785398163 corresponds to an angle of 45 degrees in radians, and the value 0.707106781 is the result of the COS function applied to the 45-degree angle.
-
Example 4 – How to calculate the value of cos (60)
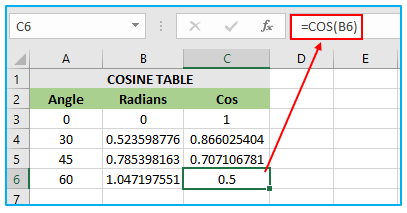
In this scenario, the angle value for which the cosine needs to be calculated is present in cell A6. The COS formula is associated with cell B6, which utilizes the RADIANS function to convert the angle value in cell A6 into radians. The result of RADIANS(A6) is 1.047197551. The COS function is applied to 1.047197551, which results in the value 0.5, and this value is assigned to cell C6.
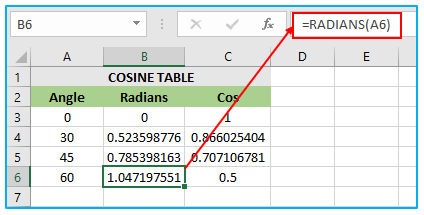
Therefore, the final value of cell C5 is 0.5, which is obtained by applying the COS function to the angle value of 1.047197551 in cell A6 after converting it to radians using the RADIANS function in cell B6. The value 1.047197551 corresponds to an angle of 60 degrees in radians, and the value 0.5 is the result of the COS function applied to the 60-degree angle.
-
Example 5 – How to calculate the value of cos (90)
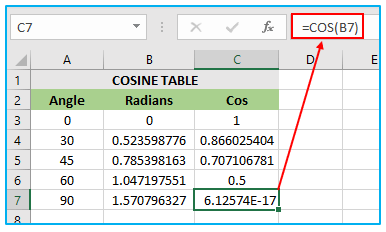
In this scenario, cell A7 contains the angle value for which the cosine needs to be calculated. The cell B7 has the COS formula with A7*PI()/180, which converts the angle value in degrees to radians. The value of PI() is 3.14159, so 90 degrees is equal to 90*(3.14159/180) = 1.570796327 radians. The COS function is applied to 1.570796327, which results in the value 6.12574E-17, and this value is assigned to cell C7.
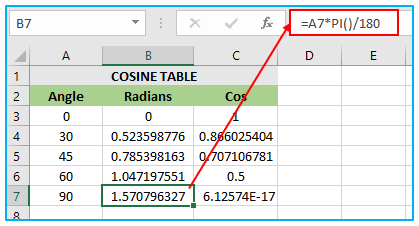
Thus, the final value of cell C7 is 6.12574E-17, which is obtained by applying the COS function to the angle value of 90 degrees in cell A7 after converting it to radians using the A7*PI()/180 formula in cell B7. The value 1.570796327 is the result of the conversion formula for 90 degrees, and the value 6.12574E-17 is the result of the COS function applied to this angle.
4. Usage of COS Function in Excel VBA:
The COS function in VBA accomplishes the same task as its counterpart in Excel: getting the cosine value of the supplied angle.
-
VBA Example 1:
Dim val1 As Double
val1 = Cos ( 0 )
val1 : 1
In this scenario, there is a variable named val1, which has been declared as a Double data type. The Double data type can hold data with double precision, which means it can store values with decimal places. The COS function has been applied to the angle value of 0, and since the cosine of 0 is 1, the resulting value has been assigned to the variable val1, which now has a value of 1.
-
VBA Example 2:
Const pi = 3.1415
Dim val As Double
‘ Convert 45 degrees to radians by multiplying by pi/180.
val = Cos (45 * pi / 180 )
‘ The variable val is now equal to 0.7071067
In this scenario, the angle value of 45 is being converted to radians using the same COS formula as in the Excel worksheet.
The COS function in Excel will return an error called “Type Mismatch” if a non-numeric value is supplied. Similarly, in Excel VBA code, if a non-numeric value is passed as an argument to the COS function, it will also return a “Type Mismatch” error.
Application of COS Function in Excel
- Trigonometric Calculations: Use the COS function to calculate the cosine of an angle, essential for trigonometry.
- Geometry: Employ COS to determine cosine values for geometric calculations involving angles and shapes.
- Physics and Engineering: Utilize COS in physics and engineering for analyzing waveforms, forces, and oscillations.
- Financial Analysis: Apply the COS function in financial modeling for complex calculations involving periodic trends.
- Scientific Research: Implement COS in scientific research for analyzing data with periodic or cyclical patterns.
- Excel Formulas: Integrate COS into Excel formulas for advanced mathematical operations and model building.
For ready-to-use Dashboard Templates:
