Quadratic Equation in Excel empowers users to solve complex mathematical problems with efficiency and accuracy. Whether you’re a student grappling with algebraic concepts or a professional engineer tackling real-world challenges, the quadratic equation solver in Excel provides a reliable solution. By leveraging Excel’s computational power, users can effortlessly manipulate coefficients and constants to find roots, analyze curves, and visualize solutions. With its intuitive interface and versatile functionality, Quadratic Equation in Excel is an indispensable tool for anyone needing to solve quadratic equations quickly and effectively. Master this feature, and unlock a world of mathematical possibilities right at your fingertips.
This Tutorial Covers:
- What is Quadratic Equation
- Goal Seek feature in Excel
- Creating a quadratic equation in Excel
- How to Solve a Quadratic Equation in Excel using Goal Seek (Step-by-Step)
- Results of Goal Seek
1. What is Quadratic Equation?
A quadratic equation is a second-degree polynomial equation with only one variable. It is typically stated as ax^2 + bx + c = 0, where x is the variable and a, b, and c are constants. The name “quadratic” derives from the Latin word “quadratus,” which means “square,” because the variable in this equation must be squared. Using the quadratic formula, completing the square, or factoring, two solutions can be discovered for quadratic equations. Algebra, calculus, physics, engineering, and finance are just a few of the mathematical and scientific fields where these equations are used.
2. Goal Seek feature in Excel:
The Goal Seek feature in Excel is a tool that allows users to find the input value needed to achieve a desired output value. This feature is useful in scenarios where you know the desired result of a formula, but not the input value required to obtain that result.
When it comes to quadratic equations, the Goal Seek feature can be used to find the roots of the equation, which are the values of x that make the equation equal to zero. By setting the output value to zero and using Goal Seek to find the input value (in this case, the value of x), you can quickly and easily find the solutions to the quadratic equation.
3. Creating a quadratic equation in Excel:
To create a quadratic equation in Excel, you need to include at least one squared variable. This can be done by multiplying the variable by itself, using the power operator ^ to calculate its second power, or using the POWER function.
The quadratic equation shown below will be applied in this example.
y=2x² + 3x – 2
You can write this formula in Excel to calculate y’s value like this:
=2*x^2+3*x-2
where x will be the reference cell in Excel. This is how an Excel quadratic equation looks.
4. How to Solve a Quadratic Equation in Excel using Goal Seek (Step-by-Step)?
The quadratic formula can be used to resolve a quadratic equation. A quadratic equation can also be resolved using Excel’s Goal Seek function.
As an illustration, consider the equation y=2×2 + 3x – 2. It is simple to determine y for any given x.
For x = 4, you can apply the below formula in cell D2.
=2*C2^2+3*C2-2
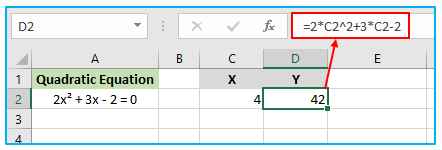
For this equation, the outcome value of y is 42, as shown in the above screen shot.
If we want to solve for x given a value of y in a quadratic equation, we can use the quadratic formula. For example, if we want to solve the equation 2x² + 3x – 2 = 12 when y is equal to 12, we can use the quadratic formula to find the value of x that satisfies this equation for y = 12.
To solve the equation 2x² + 3x – 2 = 12, we can rearrange it to standard quadratic form by subtracting 12 from both sides of the equation, which gives:
2x² + 3x – 14 = 0
Now, we can use the quadratic formula to find the solutions for x:
x = (-b ± sqrt(b² – 4ac)) / 2a
Where a = 2, b = 3, and c = -14.
Plugging in these values, we get:
x = (-3 ± sqrt(3² – 4(2)(-14))) / 2(2)
Simplifying:
x = (-3 ± sqrt(121)) / 4
x = (-3 ± 11) / 4
So, the solutions to the equation 2x² + 3x – 2 = 12 are:
x = (-3 + 11) / 4 = 2
x = (-3 – 11) / 4 = -7/2
Therefore, the solutions for x are x = 2 and x = -7/2.
Excel’s Goal Seek feature can be used to find the value of a cell that will result in a desired outcome in another cell. In this case, we can use Goal Seek to find the value of cell C2 that will result in cell D2 being equal to 12 in the quadratic equation 2x² + 3x – 2 = 12.
The steps to solve a quadratic equation using Goal Seek function in Excel are described below:
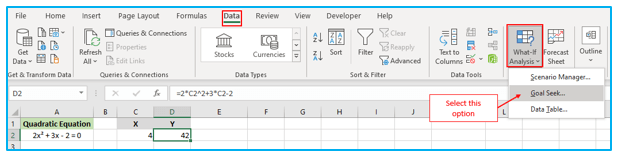
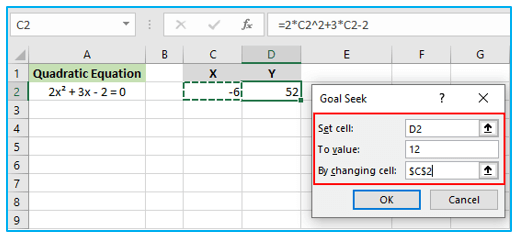
Step 1: To use Goal Seek, we need to go to the “Data” tab in Excel and click on the “What-If Analysis” option in the “Forecast” group. Then, we can select “Goal Seek” from the dropdown menu. This will bring up the “Goal Seek” dialog box.
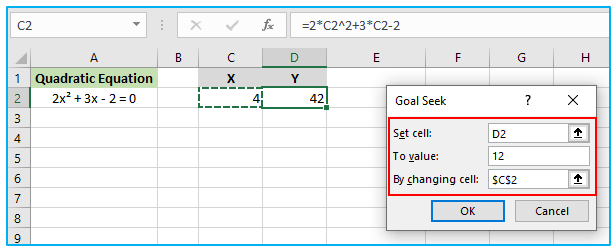
Step 2: In the “Goal Seek” dialog box, we need to select cell D2 as the cell we want to set to the desired value of 12. Then, we need to click in the “By changing cell” box and select cell C2, which represents the variable x in our quadratic equation. Finally, we can click “OK” to run the Goal Seek function.
5. Results of Goal Seek:
After running the Goal Seek function, the result looks like below:
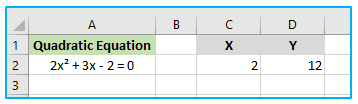
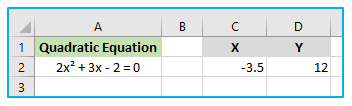
It’s worth noting that the result obtained when using Excel’s Goal Seek feature to solve quadratic equations depends on the initial value of the variable x. For the equation 2x² + 3x – 2 = 12, starting with an x-value of 1 or 4 in cell C2 gives a solution of x = 2.
However, there are two solutions to the quadratic equation, and Excel can find the other solution by starting with an x-value closer to -7/2. For instance, entering -6 into cell C2 and repeating the same steps as shown in the earlier section can give the second solution.
To find the roots of the quadratic equation (i.e., the values of x that make y=12), we can set ‘To value’ in the Goal Seek dialog box to 12. This allows Excel to solve the quadratic equation by finding the values of x that make y=12, which correspond to the x-intercepts of the quadratic curve.
The result looks like below:
Application of Quadratic Equation in Excel
- Root Calculation: Use the Quadratic Equation in Excel to find the roots (solutions) of quadratic equations, aiding in mathematical analysis and problem-solving.
- Graphical Representation: Utilize Excel’s graphing capabilities to visualize quadratic functions and their corresponding graphs, facilitating better understanding and analysis.
- Real-World Applications: Apply the Quadratic Equation in Excel to model and solve real-world problems in various fields such as physics, engineering, finance, and more.
- Optimization Problems: Solve optimization problems by utilizing the Quadratic Equation in Excel to find maximum or minimum values of quadratic functions, optimizing outcomes.
- Educational Purposes: Utilize Excel as a teaching tool to demonstrate the principles of quadratic equations and their solutions, aiding in educational instruction and learning.
- Data Analysis: Incorporate the Quadratic Equation in Excel into data analysis tasks, enabling the fitting of quadratic models to experimental or observational data for predictive purposes.
For ready-to-use Dashboard Templates:
