Calculate Standard Deviation in Excel to measure the amount of variation or dispersion in a set of values, a critical statistical tool for analysts, researchers, and data enthusiasts. Understanding how to compute this metric in Excel allows you to assess the spread of your data, whether you’re evaluating investment risks, analyzing scientific data, or measuring performance variability. This guide will lead you through the steps to accurately find the standard deviation, providing you with the insights needed to interpret your data’s consistency and predictability. By mastering this function in Excel, you’ll add a valuable analytical tool to your repertoire, enabling you to make more informed and data-driven decisions.
What is standard deviation and its use:
A standard deviation statistic assesses a dataset’s dispersion about its mean. It is determined as the variance’s square root (the spread of numbers in a dataset). When comparing data sets that may have the same mean but a distinct range, knowing the variation between each data point relative to the mean is helpful.
For example, the numbers below have a mean (average) of 20 and a standard deviation is 0 as outlined in Red
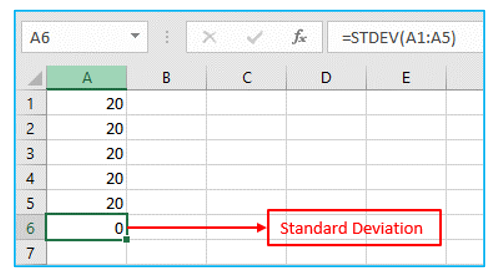
Explanation: Since all of the numbers are the same, there is no variation. The numbers therefore have a zero standard deviation. The STDEV function has been around for a while. Microsoft Excel advises utilizing the brand-new STEDV.S function to calculate standard deviation, which yields the same outcome.
1.The numbers below also have a mean (average) of 20, but standard deviation is 1.
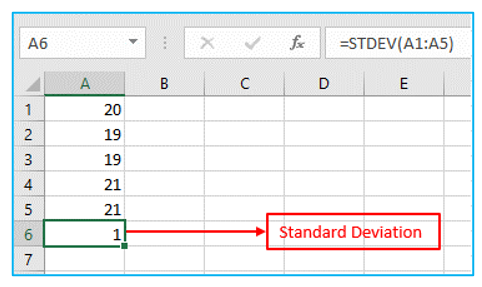
Explanation: The data are reasonably near to the mean. The numbers have a small standard deviation as a result.
2. The numbers below also have a mean (average) of 20 but standard deviation is 8.774964 as outlined in Red
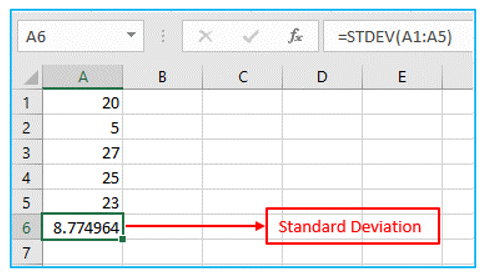
Explanation: The numbers are dispersed. The numbers have a significant standard deviation as a result.
Also Read: How to Calculate Compound Interest in Excel
How to Use Standard Deviation:
Because it may be used to gauge market volatility, standard deviation is often utilized to plan trading and investing strategies. Standard deviation is used by analysts, portfolio managers, and advisors as a fundamental risk indicator. Even the standard deviation of their mutual funds will be disclosed by investment firms.
The statistics are often simple to comprehend, which makes it useful to present them to clients and investors. Excel may be quite helpful in terms of time management by calculating and displaying the standard deviation.
Calculate Standard Deviation in Excel (standard deviation formula)
The standard deviation is simple to compute, but you must be aware of the Excel formula to use.
In Excel, we can calculate standard deviation by using six types of formulas, outlined in Blue below.
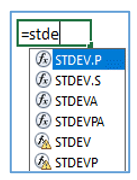
Two groups can be made up of these six formulas:
The formulas in this category are STDEV.S, STDEVA, and STDEV for calculating the sample standard deviation.
Calculating the population’s overall standard deviation: This category includes the formulas STDEV.P, STDEVPA, and STDEVP.
Let’s now comprehend these six formulas:
STDEV.S- When your information is numerical, use this. The text and logical values are disregarded.
STDEVA – When you want to include logical and text values in the calculation, use this (along with numbers). Text and FALSE are interpreted as 0, and TRUE as 1.
STDEV – Excel 2010 introduced STDEV.S. The STDEV function was utilized earlier. For backward compatibility with earlier versions, it is still present.
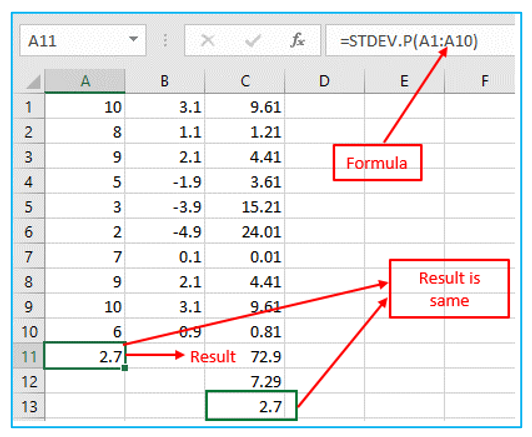
STDEV.P – The standard deviation for a sample set of data is calculated using the Excel STDEV.P function. STDEV.P uses the “n” method to calculate standard deviation while ignoring logical values and text.
STDEVPA – The Excel STDEVPA function determines the population standard deviation. STDEVPA examines text and logical that appear in references, as contrast to the STDEVP function. Use STDEVA or STDEV.S to determine standard deviation of a sample.
STDEVP – For data that represents a population, the STDEVP function determines the standard deviation. A more recent function called STDEV.P has taken the place of STDEVP and exhibits the same behavior.
Using STDEV.S Function to calculate the standard deviation
Excel’s STDEV.S function, where S stands for sample, calculates the standard deviation using a sample. Take the situation of instructing a sizable class of students. Only five pupils’ test results are available. There are 5 samples total. The formula for the STDEV.S function is as follows:
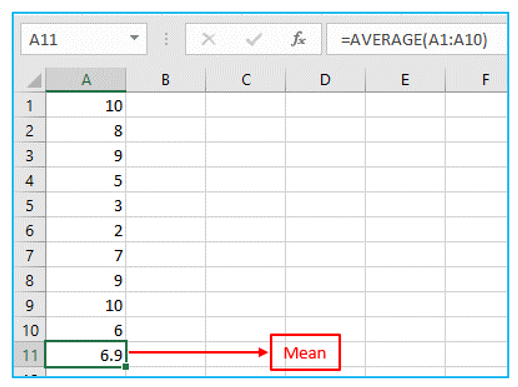
In this example, x1 = 10, x2 = 8, x3 = 9, x4 = 5, x5 = 3, x6 =2, x7 =7, x8 =9, x9 =10, x10 =6, x̄ = 6.9 (Sample mean), n = 10 (Number of data points).
Step 1: Calculate the mean (μ). Result is outlined in Red below.
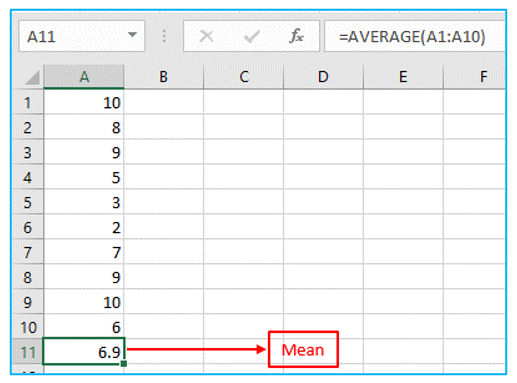
Step 2: Determine the distance to the mean for each number. Result and formula are outlined in Red below.
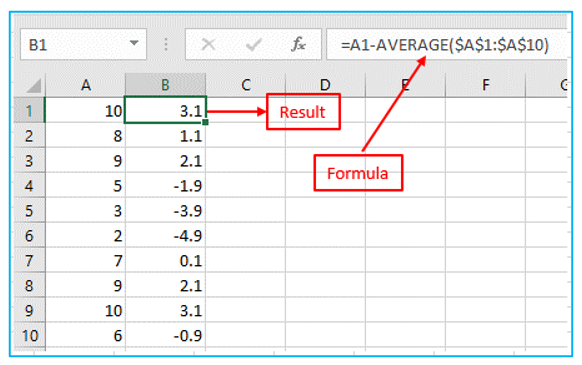
Step 3: Calculate the square of each number. Result and formula are outlined in Red below.
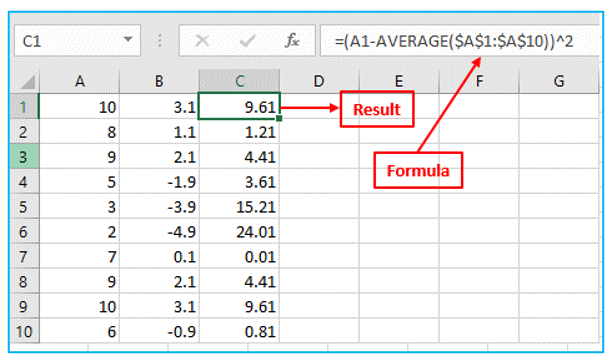
Step 4: Sum the squared numbers. Result and formula are outlined in Red below.
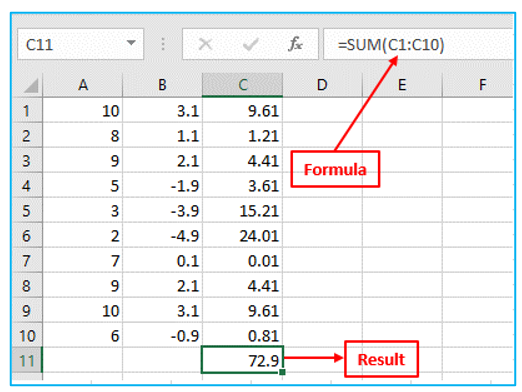
Step 5: Divide by n-1 (n=Number of data points). Result and formula are outlined in Red below.

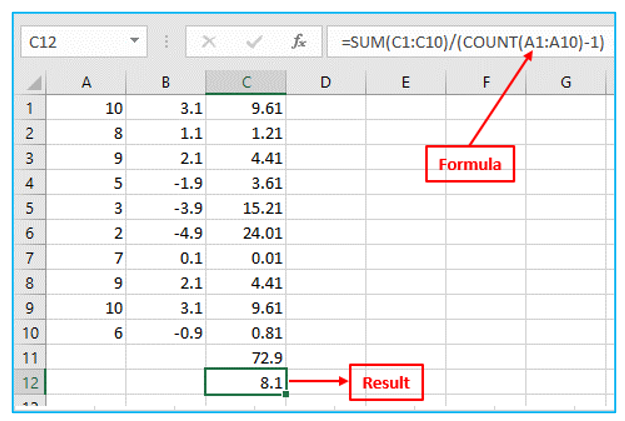
Step 6: Square root the number. Result and formula are outlined in Red below.
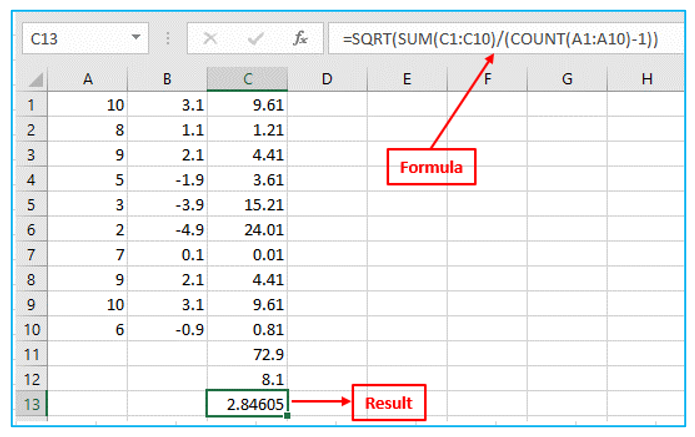
Step 7: Fortunately, Excel’s STDEV.S function can carry out each of these actions for you. Result and formula are outlined in Red below.
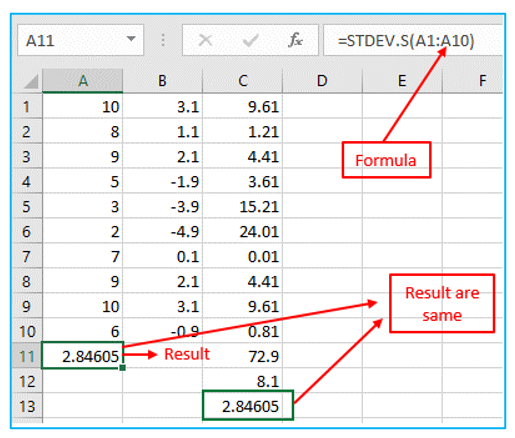
Note: When estimating the standard deviation based on a sample, why do we divide by n – 1 instead than by n? According to Bessel’s correction, multiplying by n-1 as opposed to n results in a more accurate assessment of the standard deviation.
Also Read: How to Calculate Internal Rate of Return in Excel?
Using STDEV.P Function in Microsoft Excel:
The STDEV.P function in Excel determines the standard deviation based on the entire population (the P stands for Population). Let’s say you’re selling 10 products. You have each product’s price. There are 10 data points in the population as a whole. The formula used by the STDEV.P function is as follows:
In this example, x1 = 10, x2 = 8, x3 = 9, x4 = 5, x5 = 3, x6 =2, x7 =7, x8 =9, x9 =10, x10 =6, μ = 6.9 (mean), N = 10 (Number of data points).
Step 1: Calculate the mean (μ). Result is outlined in Red below.
Step 2: Determine the distance to the mean for each number. Result and formula are outlined in Red below.

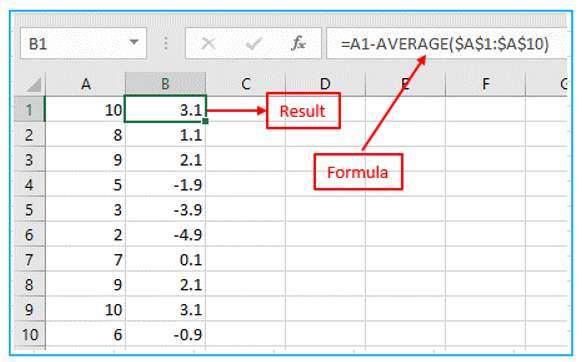
Step 3: Calculate the square of each number. Result and formula are outlined in Red below.
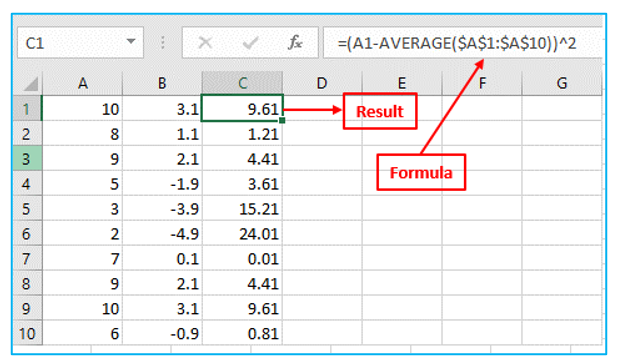
Step 4: Sum the squared numbers. Result and formula are outlined in Red below.
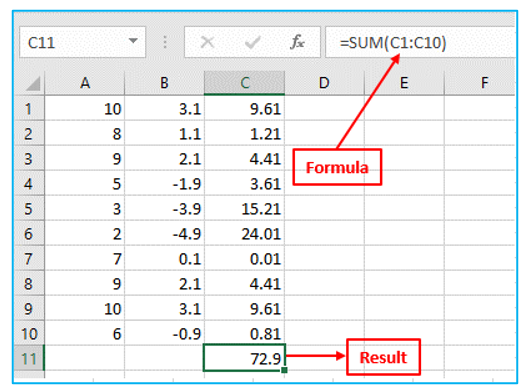
Step 5: Divide by the number of data points (n = 10). Result and formula are outlined in Red below.
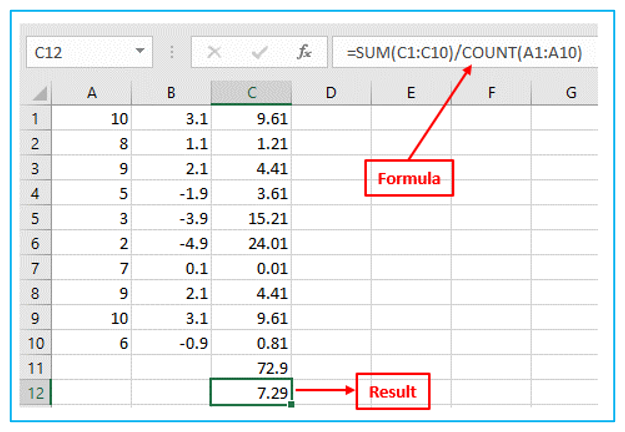
Step 6: Square root the number. Result and formula are outlined in Red below.
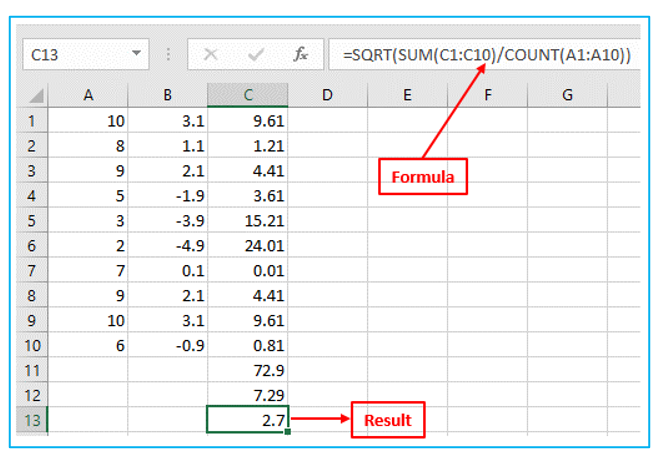
Step 7: Fortunately, Excel’s STDEV.P function can carry out each of these actions for you. Result and formula are outlined in Red below.
Elaborate VARINACE (VAR.S and VAR.P) function:
A dataset’s variability can be estimated by looking at its variance, which is a number. There is no variability when the variance is 0, meaning that each and every number in the dataset is the same. The values are more erratic as the number gets larger. The variance reveals how widely the dataset’s individual participants deviate from the mean.
Calculations of variance can be divided into two categories: sample variance and population variance.
- Population variance denotes the presence of each individual in the population in the dataset.
- Sample variance denotes the fact that a sample of the population was used to get the data.
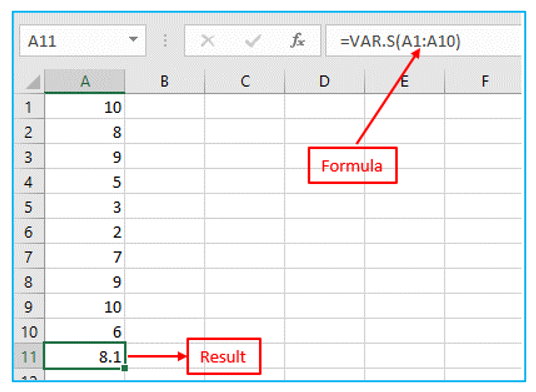
VAR.S Function: Based on a sample, the VAR.S function below calculates the variance. Result and formula are outlined in Red below.
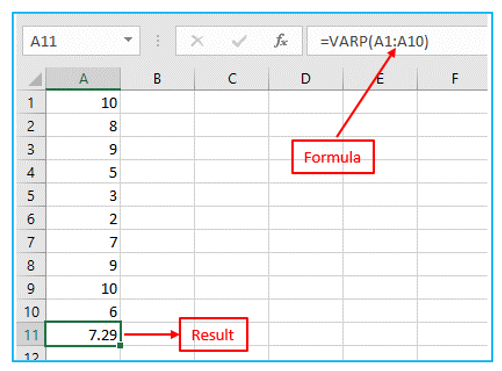
VAR.P Function: The variance is calculated using the entire population through the VAR.P function below. Result and formula are outlined in Red below.
Note: Applying the new VAR.S function is suggested in Microsoft Excel.
For ready-to-use Dashboard Templates:
